Filosofía II: Tablas de Verdad
Una tabla de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes.
Para establecer un Sistema formal se establecen las definiciones de los operadores. Las definiciones se harán en función del fin que se pretenda al construir el sistema que haga posible la formalización de argumentos:
- Como razonamiento deductivo lógico-linguistico
- Como construcción de un sistema matemático puro
- Como una aplicación lógica en un Circuito de conmutación.
Verdadero
El valor verdadero se representa con la letra
V, si se emplea notación numérica se expresa con un uno:
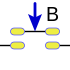
1, en un circuito eléctrico, el circuito esta cerrado.
Falso
El valor falso se representa con la letra
F, si se emplea notación numérica se expresa con un cero:
0, en un circuito eléctrico, el circuito esta abierto.
Variable
Para una variable lógica
A,
B,
C, ... que pueden ser verdaderas
V, o falsas
F, los operadores fundamentales se definen así:

Negación
La negación es un operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.

Conjunción
La conjunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad
verdadero cuando ambas proposiciones son verdaderas, y
falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderas
La tabla de verdad de la conjunción es la siguiente:

Que se corresponde con la columna 8 del algoritmo fundamental.
Disyunción
La disyunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad
verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y
falso cuando ambas son falsas.
La tabla de verdad de la disyunción es la siguiente:
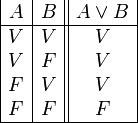
Que se corresponde con la columna 2 del algoritmo fundamental.
Implicación o Condicional
El condicional material es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad
falso sólo cuando la primera proposición es verdadera y la segunda falsa, y
verdadero en cualquier otro caso.
La tabla de verdad del condicional material es la siguiente:
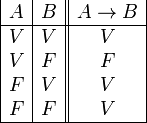
Que se corresponde con la columna 5 del algoritmo fundamental.
Bicondicional
El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad
verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad difieren.
La tabla de verdad del bicondicional es la siguiente:

Que se corresponde con la columna 7 del algoritmo fundamental.
Número de combinaciones
Partiendo de un número
n de variables, cada una de las cuales puede tomar el valor verdadero:
V, o falso:
F, por Combinatoria, podemos saber que el número total de combinaciones:
Nc, que se pueden presentar es:

el número de combinaciones que se pueden dar con
n variable, cada una de las cuales puede tomar uno entre dos valores lógicos es de dos elevado a
n, esto es, el número de combinaciones:
Nc, tiene crecimiento exponencial respecto al número de variable
n:

Si consideramos que un sistema combinacional de
n variables binarias, puede presentar un resultado verdadero:
V, o falso:
F, para cada una de las posibles combinaciones de entrada tenemos que se pueden construir
Cp circuitos posibles con
n variables de entrada, donde:

Que da como resultado la siguiente tabla:

Para componer una tabla de verdad, pondremos las
n variables en una línea horizontal, debajo de estas variables desarrollamos las distintas combinaciones que se pueden formar con
V y
F, dando lugar a la distintas
Nc, número de combinaciones. Normalmente solo se representa la función para la que se confecciona la tabla de verdad, y en todo caso funciones parciales que ayuden en su cálculo, en la figura, se pueden ver todas las combinaciones posibles
Cp, que pueden darse para el número de variables dado.

Así podemos ver que para dos variables binarias:
A y
B,
n= 2 , que pueden tomar los valores
V y
F, se pueden desarrollar cuatro combinaciones:
Nc= 4, con estos valores se pueden definir dieciséis resultados distintos,
Cp= 16, cada una de las cuales seria una función de dos variables binarias. Para otro número de variables se obtendrán los resultados correspondientes, dado el crecimiento exponencial de
Nc, cuando
n toma valores mayores de cuatro o cinco, la representación en un cuadro resulta compleja, y si se quiere representar las combinaciones posibles
Cp, resulta ya complejo para
n= 3.
Para cero variables
Un circuito sin variables, puede presentar una combinación posible:
Nc=1, con dos circuitos posibles:
Cp=2. Que serían el circuito cerrado permanentemente, y el circuito abierto permanentemente.
-
En este caso se puede ver que no interviene ninguna variable.
Cada uno de estos circuitos admite una única posición y hay dos circuitos posibles.
Para una variable
El caso de una variable binaria, que puede presentar dos combinaciones posibles:
Nc=2, con 4 circuitos posibles:
Cp=4.
| 1 | 2 | 3 | 4 |
|---|
| A | ·A | ·A | ·A | ·A |
|---|
| V | V | V | F | F |
| F | V | F | V | F |
Los casos 1 y 4 coinciden con los de cero variables, el caso 2 la salida es la de la variable y el caso 3 la negación de la variable.
Para dos variables
Considérese dos variables proposicionales
A y
B. Cada una puede tomar uno de dos valores de valores de verdad: o V (verdadero), o F (falso). Por lo tanto, los valores de verdad de
A y de
B pueden combinarse de cuatro maneras distintas: o ambas son verdaderas; o
A es verdadera y
B falsa, o
A es falsa y
B verdadera, o ambas son falsas. Esto puede expresarse con una tabla simple:

Considérese además a "
·" como una operación o funcion logica que realiza una función de verdad al tomar los valores de verdad de
A y de
B, y devolver un único valor de verdad. Entonces, existen 16 funciones distintas posibles, y es fácil construir una tabla que muestre qué devuelve cada función frente a las distintas combinaciones de valores de verdad de
A y de
B.
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|
| A | B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B | A·B |
|---|
| V | V | V | V | V | V | V | V | V | V | F | F | F | F | F | F | F | F |
| V | F | V | V | V | V | F | F | F | F | V | V | V | V | F | F | F | F |
| F | V | V | V | F | F | V | V | F | F | V | V | F | F | V | V | F | F |
| F | F | V | F | V | F | V | F | V | F | V | F | V | F | V | F | V | F |
Las dos primeras columnas de la tabla muestran las cuatro combinaciones posibles de valores de verdad de A y de B. Hay por lo tanto 4 líneas, y las 16 columnas despliegan todos los posibles valores que puede devolver una función "
·".
De esta forma podemos conocer mecánicamente, mediante algoritmo, los posibles valores de verdad de cualquier conexión lógica interpretada como función, siempre y cuando definamos los valores que devuelva la función.
Se hace necesario, pues, definir las funciones que se utilizan en la confección de un sistema lógico.
De especial relevancia se consideran las definiciones para el Calculo
de deducción natural y las
puertas lógicas en los circuitos electrónicos.
Tablas de verdad
Las tablas nos manifiestan los posibles valores de verdad de cualquier proposición molecular, así como el análisis de la misma en función de las proposicíones que la integran, encontrándonos con los siguientes casos:
Verdad Indeterminada o Contingencia
Se entiende por verdad contingente, o verdad de hecho, aquella proposición que puede ser verdadera o falsa, según los valores de las proposiciones que la integran. Sea el caso:

.
Su tabla de verdad se construye de la siguiente manera:
Ocho filas que responden a los casos posibles que pueden darse según el valor
V o
F de cada una de las proposiciones A, B, C.
(Columnas 1, 2, 3)
Una columna
(Columna 4) en la que se establecen los valores de

aplicando la definición del disyuntor a los valores de B y de C en cada una de las filas.
(Columnas 2,3 → 4)
Una columna
(columna 5) en la que se establecen los valores resultantes de aplicar la definición de la conjunción entre los valores de A
(columna 1) y valores de la columna

,
(columna 4) que representarán los valores de la proposición completa

, cuyo valor de verdad es
V o
F según la fila de los valores de A, B, y C que consideremos.
(Columnas 1,4 → 5)
Donde podemos comprobar cuándo y por qué la proposición

es
V y cuándo es
F.
-
Contradicción
Se entiende por proposición contradictoria, o contradicción, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es F. Dicho de otra forma, su valor F no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso:

Procederemos de manera similar al caso anterior. Partiendo de la variable
A y su contradicción, la conjunción de ambos siempre es falso, dado que si
A es verdad su contradicción es falsa, y si
A es falsa su contradicción es verdad, la conjunción de ambas da falso en todos los casos.
Tautologías
Se entiende por proposición tautológica, o tautología, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es V. Dicho de otra forma, su valor V no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso:

Siguiendo la mecánica algorítmica de la tabla anterior construiremos su tabla de verdad, tenemos la variable
A en disyunción con su contradicción, si
A es verdad, su negación es falsa y si
A es falsa su negación es verdad, en cualquier caso una de las dos alternativas es cierta, y su disyunción es cierta en todos los casos.






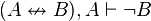
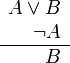



![[(p\or q)\wedge \neg p]\supset q](http://upload.wikimedia.org/wikipedia/es/math/b/c/6/bc6343138457fd7051fffe5e01747079.png)
![[(p\nleftrightarrow q)\wedge \neg p]\supset q](http://upload.wikimedia.org/wikipedia/es/math/d/9/b/d9b6a826944e21572cbb351cd74a4466.png)


![[(p\rightarrow q)\wedge \neg q]\rightarrow \neg p](http://upload.wikimedia.org/wikipedia/es/math/a/4/e/a4e09e9b1ab3ae07f10000aef2e3f871.png)























 .
. aplicando la definición del disyuntor a los valores de B y de C en cada una de las filas.(Columnas 2,3 → 4)
aplicando la definición del disyuntor a los valores de B y de C en cada una de las filas.(Columnas 2,3 → 4)