Filosofía II: Reglas de Inferencia
En lógica, especialmente en lógica matemática, una
regla de inferencia es un esquema para construir inferencias válidas. Estos esquemas establecen relaciones sintácticas entre un conjunto de fórmulas llamados
premisas y una aserción llamada
conclusión.
Estas relaciones sintácticas son usadas en el proceso de inferencia, por el que se llega a nuevas aserciones verdaderas a partir de otras ya conocidas. Las reglas también se aplican a la lógica informal y a las discusiones, pero la formulación es mucho más difícil y polémica.
Como se mencionó, la aplicación de una regla de inferencia es un procedimiento puramente sintáctico. Sin embargo, debe también ser el válido, o mejor dicho, preservar la validez. Para que el requisito de preservación de la validez tenga sentido, es necesaria una cierta forma semántica para las aserciones de las reglas de inferencia y las reglas de inferencia en sí mismas.
Reglas de inferencia clásicas
Algunas de las reglas de inferencia más conocidas son:
En la lógica proposicional:
Generalmente abreviado
MPP o
MP, es una regla de inferencia que tiene la siguiente forma:
- Si A, entonces B
- A
- Por lo tanto, B
Por ejemplo, un razonamiento que sigue la forma del modus ponens podría ser:
- Si está soleado, entonces es de día.
- Está soleado.
- Por lo tanto, es de día.
Otra manera de presentar el modus ponens con el condicional es:

Y aún otra manera es a través de la notación del cálculo de secuentes: Con condicional:

Es una forma válida de argumento que dice:
- O bien A, o bien B
- A
- Por lo tanto, no B
Por ejemplo, un razonamiento que sigue la forma del modus ponendo tollens podría ser:
- O bien es de día, o bien es de noche.
- Es de día.
- Por lo tanto, no es de noche.
Otra manera de presentar el modus ponendo tollens es:

Y aún otra manera es a través de la notación del cálculo de secuentes:
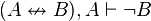
MTP, es una forma válida de argumento:
- es el caso que A, o es el caso que B
- No A
- Por lo tanto, B
o exclusivo:
- O es el caso que A, o es el caso que B
- No A
- Por lo tanto, B
Por ejemplo, un razonamiento que sigue la forma del silogismo disyuntivo exclusivo podría ser:
- O es de día o es de noche.
- No es de día.
- Por lo tanto, es de noche.
Otra manera de presentar el silogismo disyuntivo es:
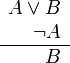
o exclusivo

Y aún otra manera es a través de la notación del cálculo de secuentes:

o exclusivo

En lógica proposicional su representación sería la siguiente :
![[(p\or q)\wedge \neg p]\supset q](http://upload.wikimedia.org/wikipedia/es/math/b/c/6/bc6343138457fd7051fffe5e01747079.png)
y exclusivo:
![[(p\nleftrightarrow q)\wedge \neg p]\supset q](http://upload.wikimedia.org/wikipedia/es/math/d/9/b/d9b6a826944e21572cbb351cd74a4466.png) MTT
MTT o
MT, es una regla de inferencia que tiene la siguiente forma:
- si A entonces B
- No B
- Por lo tanto, no A
Por ejemplo, un razonamiento que sigue la forma del modus tollens podría ser:
- Si llovió, entonces el suelo está mojado.
- El suelo no está mojado.
- Por lo tanto, no llovió.
Es importante evitar caer en el razonamiento incorrecto de:
- Sólo si es mayor de edad entonces tiene permiso de conducir
- No tiene permiso de conducir
- Por lo tanto, no es mayor de edad.
Es incorrecto puesto que podría ser mayor de edad y no tener permiso de conducir, de ahí la importancia de no confundir la implicación (si p, entonces q) con el condicional (p si y solo si q), es decir, p es condición para que se pueda dar q, pero p no implica necesariamente q (ser mayor de edad es condición necesaria, pero no suficiente para tener permiso de conducir).
Otra manera de presentar el modus tollens es:

Y aún otra manera es a través de la notación del cálculo de secuentes:

En lógica proposicional su representación sería la siguiente :
![[(p\rightarrow q)\wedge \neg q]\rightarrow \neg p](http://upload.wikimedia.org/wikipedia/es/math/a/4/e/a4e09e9b1ab3ae07f10000aef2e3f871.png)
En la lógica de primer orden:
- Regla de Generalización universal
En la lógica modal:
![[(p\or q)\wedge \neg p]\supset q](http://upload.wikimedia.org/wikipedia/es/math/b/c/6/bc6343138457fd7051fffe5e01747079.png)
![[(p\nleftrightarrow q)\wedge \neg p]\supset q](http://upload.wikimedia.org/wikipedia/es/math/d/9/b/d9b6a826944e21572cbb351cd74a4466.png)
![[(p\rightarrow q)\wedge \neg q]\rightarrow \neg p](http://upload.wikimedia.org/wikipedia/es/math/a/4/e/a4e09e9b1ab3ae07f10000aef2e3f871.png)



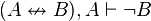
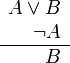





Excelente, me sacó de muchas dudas
ResponderEliminar