Filosofía II: Probabilidad

Filosofía II: Probabilidad

                                La probabilidad es una medición numérica que va de 0 a 1 de la posibilidad de que un evento ocurra. Si da cerca de 0 es improbable que ocurra el evento y si da cerca de uno es casi seguro que ocurra.
P (a): nº de resultados en que ocurra a
Nº de resultados posibles

Tipos de sucesos

• Exhaustivo: se dice que dos o más sucesos son exhaustivos si se consideran todos los posibles resultados.

Simbólicamente: p (A o B o...) = 1

• No exhaustivos: se dice que dos o más sucesos son exhaustivos si no cubren todos los posibles resultados.
• Mutuamente excluyentes: sucesos que no pueden ocurrir en forma simultánea:

P(A y B) = 0 y p(A o B) = p(A) + p (B)
Ejemplo: hombres, mujeres

• No mutuamente excluyentes: sucesos que pueden ocurrir en forma simultánea:

P (A o B) = p (A) + p (B) ? p (A y B)
Ejemplo: hombres, ojos cafés

• Independientes: Sucesos cuya probabilidad no se ve afectada por la ocurrencia o no ocurrencia del otro :

P ( AI B ) = P ( A ); P ( BIA ) = P (B) Y P (A Y B) = P(A) P(B)
Ejemplo: sexo y color de ojos

• Dependientes: sucesos cuya probabilidad cambia dependiendo de la ocurrencia o no ocurrencia del otro:

P ( AI B ) difiere de p (A); P ( BIA ) difiere de P(B);
Y P (A Y B)= P ( A ) P ( BIA )= P (B) P ( AI B )
Ejemplo: raza y color de ojos

Distribución maestral
El diagrama de árbol es muy útil para visualizar las probabilidades condicional y conjunta y en particular para el análisis de decisiones administrativas que involucran varias etapas.
EJEMPLO: una bolsa contiene 7 fichas rojas (R) y 5 azules (B), se escogen 2 fichas, una después de la otra sin reemplazo. Construya el diagrama de árbol con esta información.

Distribuciones de probabilidad:
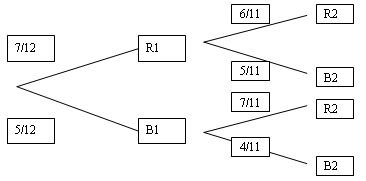
Variables aleatorias: es la descripción numérica del resultado de un experimento. Puede ser:

2. Variable aleatoria discreta: puede tomar una secuencia de valores finita o infinita.
3. Variable aleatoria continua: puede tomar cualquier valor en un intervalo o en una colección de intervalos. Ejemplo, peso, tiempo, temperatura.

1. Variables aleatorias discretas:

Indicadores:

• Valor esperado , esperanza matemática o media: es un promedio ponderado de los valores posibles de la variable aleatoria. Para esto debemos multiplicar cada uno de los valores de la variable aleatoria por su probabilidad y luego sumar los resultados.

E (x) : µ : ∑ xf (x)

• Varianza: nos da una medida de la dispersión o de la variabilidad de la variable aleatoria con respecto al media. Se trata de un promedio ponderado de las desviaciones cuadráticas de la media µ

σ 2 : ∑ ( x - µ) 2 f (x)

• Desvió estándar: es la raíz cuadrada de la varianza

√σ 2

Cuando mayor es la desviación estándar mayor es la dispersión de datos alrededor de la media.
Ejemplo integrador

Numero de llamadas (x)	Probabilidad f (x)	Esperanza µ o media	Varianza σ 2 (x1 - µ) 2 * f (x)	Desvió estándar √ σ 2
0	0.1	0	0.60
1	0.15	0.15	0.31
2	0.3	0.6	0.060
3	0.2	0.6	0.060
4	0.15	0.6	0.36
5	0.10	0.5	0.65
	µ	2.45	2.04 σ 2	1.42

Distribución binomial: se utiliza para calcular la probabilidad de x éxitos en n intentos.
Características:

• ensayos idénticos. (N ensayos de bernoulli idénticos)
• En cada ensayo hay dos resultados. Acierto o fracaso.
• Las probabilidades de los dos resultados no se modifican de un ensayo a otro. Y es constante de prueba a prueba
• Los ensayos son independientes, es decir que el resultado de un ensayo no afecta el resultado del siguiente.

En un lenguaje más formal, el símbolo p representa la probabilidad de un éxito y el símbolo q ( 1- p ) representa la probabilidad de un fracaso. Para representar cierto número de éxitos, utilizaremos el símbolo r y para simbolizar el número total de ensayos emplearemos el símbolo n.

n: numero de intentos
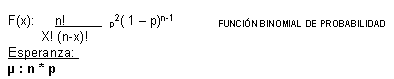
p: probabilidad de acierto
X: numero de aciertos en n intentos f x: probabilidad de x aciertos en n intentos.
Varianza:
σ 2 : n * p (1 ? p)
Distribución hipergeométrica:
la probabilidad de aciertos difiere de acuerdo a las sacadas de una bolsa. ( dif con la distribución anterior)
Distribución de Poisson: se utiliza para calcular la p de x ocurrencias en un intervalo específico de tiempo, espacio o volumen.

• La p de ocurrencia de un evento es la misma para cualquiera de 2 intervalos de igual valor.
• La ocurrencia o no ocurrencia del evento en cualquier intervalo es independiente.

Función de probabilidad de Poisson:

λ : es el número de ocurrencias en un intervalo o valor esperado.
E: 2.71828
X: nº de ocurrencias dentro de un intervalo
Fx: probabilidad de x ocurrencia.
Variables aleatorias continuas.
Distribución normal: tiene forma de campana y esta determinada por la media y la desviación estándar.
La distribución normal estándar tiene una media igual a cero y un desvió estándar igual a uno
Características de la distribución normal de la probabilidad.
1. La curva tiene un solo pico, por consiguiente es uní modal. Presenta una forma de campana.
2. La media de una población distribuida normalmente se encuentra en el centro de su curva normal.
3. A causa de la simetría de la distribución normal de probabilidad, la mediana y la moda de la distribución también se hallan en el centro, por tanto en una curva normal, la media, la mediana y la moda poseen el mismo valor.
4. Las dos colas (extremos) de una distribución normal de probabilidad se extienden de manera indefinida y nunca tocan el eje horizontal.
Áreas bajo la curva normal.
El área total bajo la curva normal será de 1.00 por lo cual podemos considerar que las áreas bajo la curva son probabilidades.
El valor de Z.
Z= Número de desviaciones estándar de x respecto a la media de esta distribución.
Z: x - µ
σ
X=valor de la variable aleatoria que nos interesa.
 = media de la distribución de esta variable aleatoria.
 = desviación estándar de esta distribución.
Las variables aleatorias distribuidas en forma normal asumen muchas unidades diferentes de medición, por lo que hablaremos de forma estándar y les daremos el símbolo de Z.
Distribución exponencial: es útil para describir el tiempo para determinar una tarea o el tiempo entre ocurrencias de un evento.
F(x): 1 e ?x/ µ
µ